Four Quadrants: Difference between revisions
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
===The Four Quadrants=== | ===The Four Quadrants=== | ||
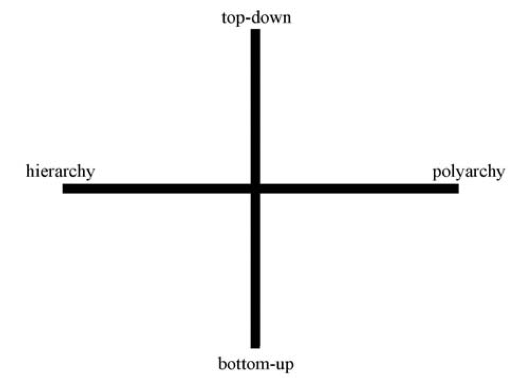
In his article, The Fourth Quadrant, Professor Zittrain develops a four quadrant framework for thinking about the Internet. This framework looks at two criteria: (1) how generative something is, and (2) how singular it is. | |||
The generativity of a phenomena is assessed on a scale from entirely “top-down” to entirely “bottom-up.” The range of singularity runs from “hierarchy” to “polyarchy.” This is captured in the following chart from the article: | |||
[[Image:Zittrain Four Quadrants.png]] | |||
Professor Zittrain uses precise (sometimes unconventional) definitions of these terms: | |||
*• Top-down: systems in which “there is a separation between those who make the rules and those who live under them . . . .” | |||
*• Bottom-up: systems where the rules can come from any person without separation between the people who make the rules and people who live under them. | |||
*• Hierarchy: “a system for which there is no alternative, either because it does not exist, because it would be too costly, or because law precludes it.” | |||
*• Polyarchy: being able to choose between multiple regimes or systems. | |||
== Proposals == | == Proposals == | ||
Revision as of 14:08, 19 December 2010
Introduction
Terms
Definitions
The Four Quadrants
In his article, The Fourth Quadrant, Professor Zittrain develops a four quadrant framework for thinking about the Internet. This framework looks at two criteria: (1) how generative something is, and (2) how singular it is.
The generativity of a phenomena is assessed on a scale from entirely “top-down” to entirely “bottom-up.” The range of singularity runs from “hierarchy” to “polyarchy.” This is captured in the following chart from the article:
Professor Zittrain uses precise (sometimes unconventional) definitions of these terms:
- • Top-down: systems in which “there is a separation between those who make the rules and those who live under them . . . .”
- • Bottom-up: systems where the rules can come from any person without separation between the people who make the rules and people who live under them.
- • Hierarchy: “a system for which there is no alternative, either because it does not exist, because it would be too costly, or because law precludes it.”
- • Polyarchy: being able to choose between multiple regimes or systems.